hujan di kala senja: April 2020

Single Linked List Pada C++

Single Linked List merupakan suatu bentuk struktur data yang berisi kumpulan data yang disebut sebagai node yang tersusun secara sekuensial, saling sambung menyambung, dinamis, dan terbatas. Cara untuk menghubungkan satu node dengan node lainnya maka Linked List menggunakan pointer sebagai penunjuk node selanjutnya.

Node merupakan sebuah struct atau tipe data bentukkan yang menempati suatu lokasi memori secara dinamis yang terdiri dari beberapa field, minimal 2 buah field. Field tersebut adalah field untuk isi struct datanya sendiri dan 1 field arbitari bertipe pointer sebagai penunjuk node selanjutnya.

struct tnode {

int value;

struct tnode *next;

}

struct tnode *head = 0;

Kenapa menggunakan Linked List? Kenapa tidak menggunakan Array?

Array merupakan salah satu variabel yang bersifat statis (ukuran dan urutannya sudah pasti). Selain itu, ruang memori yang dipakai oleh array tersebut tidak dapat dihapus bila array tersebut sudah tidak digunakan lagi pada saat program dijalankan. Setiap ingin menambahkan data, anda akan selalu menggunakan variabel pointer yang baru, maka akibatnya anda akan sangat banyak membutuhkan sebuah variabel pointer. Oleh karena itu sebaiknya menggunakan satu variabel pointer saja untuk menyimpan banyak data dengan menggunakan metode yang kita sebut dengan Single Linked List atau Linked List.

Perbedaan Array dan Linked List

Array:
- Statis
- Penambahan dan penghapusan data terbatas
- Random access
- Penghapusan Array tidak mungkin

Linked List:
- Dinamis
- Penambahan dan penghapusan tidak terbatas
- Sequential access
- Penghapusan mudah

Pembuatan Single Linked List

1. Membuat struct node

struct TNode{

int data;

TNode *next;

}

Pembuatan struct bernama TNode yang berisi 2 field, yaitu pada field pertama dengan variabel data dengan tipe data integer dan field kedua yaitu next yang bertipe pointer dari TNode. Setelah selesai pembuatan struct, selanjutnya buat variabel head yang bertipe pointer dari TNode yang berguna untuk sebagai kepala dari linked list.

2. Membentuk node baru

Untuk pembentukan atau pembuatan node baru dapat menggunakan keyword new yang berarti untuk mempersiapkan sebuah node baru beserta alokasi memorinya, kemudian node tersebut akan di isi data dan kemudian pointer nextnya akan ditunjuk ke NULL.

TNode *baru;
baru = new TNode;
baru->data = databaru;
baru->next = baru;

3. Single Linked List menggunakan head

Deklarasi Pointer penunjuk kepala Single Linked List manipulasi Linked List tidak bisa dilakukan langsung ke node yang dituju, melainkan harus menggunakan suatu pointer penunjuk terlebih dahulu ke node pertama didalam linked list. Deklarasinya sebagai berikut:

TNode *head;

Fungsi Insialisasi Single Linked List

void int(){
read = NULL;
}

Function untuk mengetahui kosong atau tidaknya didalam Single Linked List jika pointer head tidak menunjuk pada suatu node maka kosong.

int isEmpty(){

if(head == NULL) return 1;

else return 0;

}

4. Penambahan data pada Single Linked List

Pada konsepnya adalah untuk mengkaitkan node baru dengan pointer atau head, yang kemudian head tersebut akan menunjuk pada data baru tersebut sehingga head akan tetap selalu menjadi data terdepan.

Setiap node pada linked list mempunyai field yang berisi pointer ke node berikutnya, dan juga memiliki field yang berisi data. pada akhir linked list, node terakhir menunjuk ke node terdepan sehingga linked list tersebut berputar, lalu node terakhir menunjuk lagi ke head.

Penghapusan data pada Single Linked List

Penghapusan node tidak boleh dilakukan jika keadaan node sedang ditunjuk oleh pointer, maka harus dilakukan penunjukan terlebih dahulu dengan variabel hapus pada head, kemudian dilakukan pergeseran ke node berikutnya sehingga data setelah head menjadi head baru.

struct tnode *curr = head;

// if x is in head node

if ( head->value == x ) {

head = head->next;

free(curr);

}

// if x is not in head node, find the location

else {

while ( curr->next->value != x ) curr = curr->next;

struct tnode *del = curr->next;

curr->next = del->next;

free(del);

}

Stack and Queue

Stack dan Queue keduanya adalah struktur data non-primitif. Perbedaan utama antara stack dan antrian adalah bahwa stack menggunakan metode LIFO (last in first out) untuk mengakses dan menambahkan elemen data sedangkan Antrian menggunakan metode FIFO (First In First Out) untuk mengakses dan menambahkan elemen data.
Definisi tumpukan (Stack)

Stack adalah struktur data linier non-primitif. Ini adalah daftar yang dipesan di mana item baru ditambahkan dan elemen yang ada dihapus hanya dari satu ujung, disebut sebagai bagian atas tumpukan (TOS). Karena semua penghapusan dan penyisipan dalam tumpukan dilakukan dari atas tumpukan, elemen terakhir yang ditambahkan akan menjadi yang pertama dihapus dari tumpukan. Itulah alasan mengapa tumpukan disebut jenis daftar Last in first out (LIFO). Elemen yang sering diakses di tumpukan adalah elemen paling atas, sedangkan elemen terakhir dibagian bawah tumpukan.

Contoh: Jika anda berasumsi hanya satu sisi penutup sobek, dan biskuit dikeluarkan satu persatu. Ini disebut popping, dan jika anda ingin menyimpan beberapa biskuit tersebut untuk beberapa waktu kemudian, anda memasukkannya kembali ke dalam bungkusan melalui ujung yang sama yang disebut mendorong.

Definisi Antrian (Queue)
Antrian adalah struktur data linier yang masuk dalam kategori tipe non-primitif. Ini adalah kumpulan elemen sejenis. Penambahan elemen baru terjadi di satu ujung yang disebut ujung belakang. Demikian pula, penghapusan elemen yang ada terjadi di ujung lain yang disebut Front-end, dan secara logis jenis Pertama masuk pertama keluar (FIFO) daftar.

Contoh:

Dalam kehidupan sehari hari, kita menemukan banyak situasi di mana kita keluar untuk menunggu layanan yang di inginkan, dan di sana kita harus masuk ke antrian menunggu giliran kita untuk dilayani.

Perbedaan utama antara tumpukan dan antrian:
1. Stack mengikuti mekanisme LIFO di sisi lain. Antrian mengikuti mekanisme FIFO untuk menambah dan menghapus elemen.
2. Dalam tumpukan, ujung yang sama digunakan untuk menyisipkan dan menghapus elemen. Sebaliknya, dua ujung yang berbeda digunakan dalam antrian untuk menyisipkan dan menghapus elemen.
3. Stack hanya memiliki satu ujung terbuka yang merupakan alasan untuk menggunakan hanya satu pointer untuk merujuk ke bagian atas tumpukan. Tetapi antrian menggunakan dua pointer untuk merujuk depan dan ujung belakang antrian.4. Stack melakukan dua operasi yang dikenal sebagai push dan pop sedangkan dalam Queue dikenal sebagai enqueue dan dequeue.
5. Antrian memiliki varian seperti antrian bundar, antrian prioritas, antrian berakhir ganda, dll. Sebaliknya, tumpukan tidak memiliki varian.
Operasi di Stack:
PUSH: ketika elemen baru ditambahkan ke bagian atas tumpukan dikenal sebagai operasi Push. Mendorong suatu elemen di tumpukan meminta penambahan elemen, karena elemen baru akan dimasukkan di bagian atas. Setelah setiap operasi push, bagian atas dinaikkan satu. Jika array penuh, dan tidak ada elemen baru dapat ditambahkan, itu disebut kondisi Stack Full atau Stack Overflow. int stack[5], top = -1

void push()
{
int item;
if (top<4)
{
printf("Enter the number");
scan("%d, &item);
top=top+1;
stack[top]=item;
}
else
{
printf("Stack is full");
}
}

POP: Ketika suatu elemen dihapus dari atas tumpukan itu dikenal sebagai operasi POP. Tumpukan berkurang satu, setelah setiap operasi pop. Jika tidak ada elemen yang tersisa di tumpukan dan pop dilakukan, maka ini akan menghasilkan kondisi Stack Underflow yang berarti tumpukan kosong.
int stack[5] = -1
void pop()
{
if(top>=4)
{
item=top-1;
top=top-1;
printf("Number deleted is=%d", item);
}
else
{
printf("Stack is empty");
}
}

Operasi di Queue

Enqueue: Untuk menyisipkan elemen dalam antrian.
int queue[5], Front=-1 and rear=-1;
void add()
{
int item;
if(rear<4)
{
printf(Enter the number");
scan("%d,&item);
if(front==-1)
{
front=0;
rear=0;
}
else
{
rear=rear+1;
}
queue[rear]=item;
}
else
{
printf("Queue is full");
}
}

Dequeue: Untuk menghapus elemen dari antrian.
int queue[5], Front=-1 and rear=-1;
void delete()
{
int item;
if(front !=-1)
{
item=queue[front];
if(front==rear)
{
front=-1;
rear=-1;
}
else
{
front=front+1;
print("Number deleted is=%d", item);
}
}
else
{
printf("Queue is empty");
}
} Hashing Tabel, and Binary Tree

Hashing adalah teknik yang digunakan untuk menyimpan dan mengambil kunci dengan cepat. Dalam hashing, string karakter ditransformasikan menjadi nilai panjang yang biasanya lebih pendek atau kunci yang mewakili string asli. Hashing digunakan untuk mengindeks dan mengambil item dalam database karena lebih cepat menemukan item menggunakan kunci hash yang lebih pendek daripada menemukannya menggunakan nilai asli. Hashing juga dapat didefinisikan sebagai konsep mendistribusikan kunci dalam array yang disebut tabel hash menggunakan fungsi yang ditentukan yang disebut fungsi hash. Hash Table

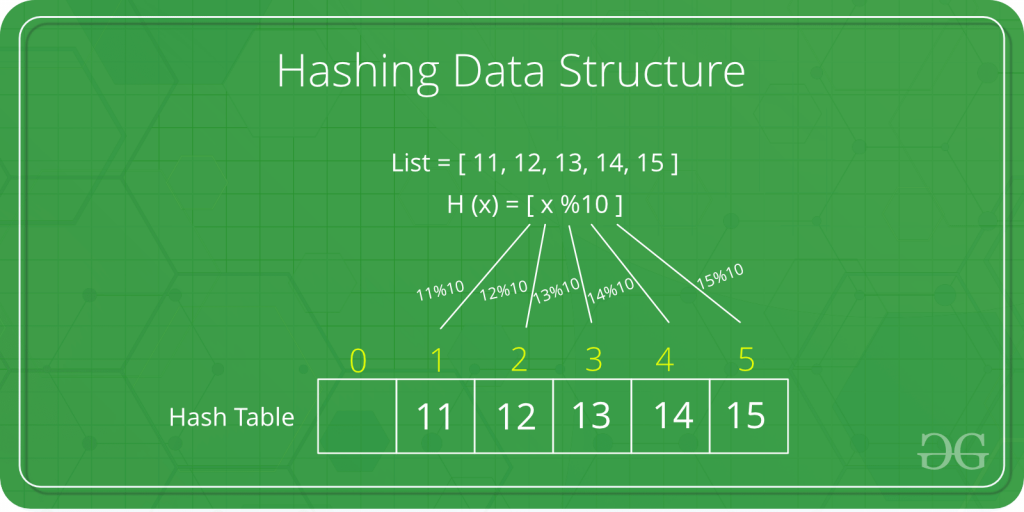
Hash table adalah struktur data yang mengimplementasikan tipe data abstrak array asosiatif, struktur yang dapat memetakan kunci ke nilai. Tabel hash menggunakan fungsi hash untuk menghitung indeks, juga disebut kode hash, ke dalam array dari ember atau slot, dari mana nilai yang diinginkan dapat ditemukan.

Tree

Tree adalah abstract data type (ADT) yang banyak digunakan untuk mensimulasikan struktur hierarki pohon, dengan nilai root dan subtrees of children dengan node parent, direpresentasikan sebagai satu set node yang terhubung. Struktur data pohon dapat didefinisikan secara rekursif sebagai kumpulan node (dimulai dari simpul akar), di mana setiap simpul adalah struktur data yang terdiri dari suatu nilai, bersama dengan daftar referensi ke node (Anak), dengan kendala yang tidak ada referensi digandakan, dan tidak ada yang menunjuk ke root.

Binary Tree

Merupakan salat satu bentuk struktur data tidak linier yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul / node dengan satu elemen khusus yang disebut root dan node lainnya terbagi menjadi himpunan yang tak saling berhubungan satu sama lainnya (disebut subtree). dibawah ini diuraikan istilah-istilah umum dalam tree.

Parent : predecssor satu level di atas suatu node.
Child : successor satu level di bawah suatu node.
Sibling : node-node yang memiliki parent yang sama dengan suatu node.
Subtree : bagian dari tree yang berupa suatu node beserta descendantnya dan memiliki semua karakteristik dari tree tersebut.
Size : banyaknya node dalam suatu tree.
Height : banyaknya tingkatan/level dalam suatu tree.
Root : satu-satunya node khusus dalam tree yang tak punya predecssor.
Leaf : node-node dalam tree yang tak memiliki seccessor.
Degree : banyaknya child yang dimiliki suatu node.

Prefix : *+ab/-cde

Postfix : ab+cd-e/*

Infix : (a+b)*((c-d)/e)

Pengertian Binary Tree dalam Struktur Data
Pohon biner adalah pohon dengan syarat bahwa tiap node hanya memiliki boleh maksimal dua subtree dan kedua subtree tersebut harus terpisah. Sesuai dengan definisi tersebut, maka tiap node dalam binary tree hanya boleh memiliki paling banyak dua anak.

Node pada Binary Tree

Jumlah maksimum node pada setiap tingkat adalah 2n, Node pada binary tree maksimumnya berjumlah 2n-1.

Hitung jumlah node dalam tree

int count(Node *root)

{

if(root==NULL)

return 0;

else

return count(root->kiri)+ count(root->kanan)+1;

}

Jika root bernilai NULL, Artinya tree masih kosong, maka akan memberikan nilai balik berupa 0. Sebaliknya, jika root tidak bernilai NULL maka penghitungan jumlah node dalam tree dilakukan dengan cara mengunjungi setiap node, dimulai dari root ke subtree kiri, kemudian ke subtree kanan dan masing-masing node dicatat jumlahnya, dan terakhir jumlah node yang ada di subtree kiri dijumlahkan dengan jumlah node yang ada di subtree kanan ditambah 1 yaitu node root.

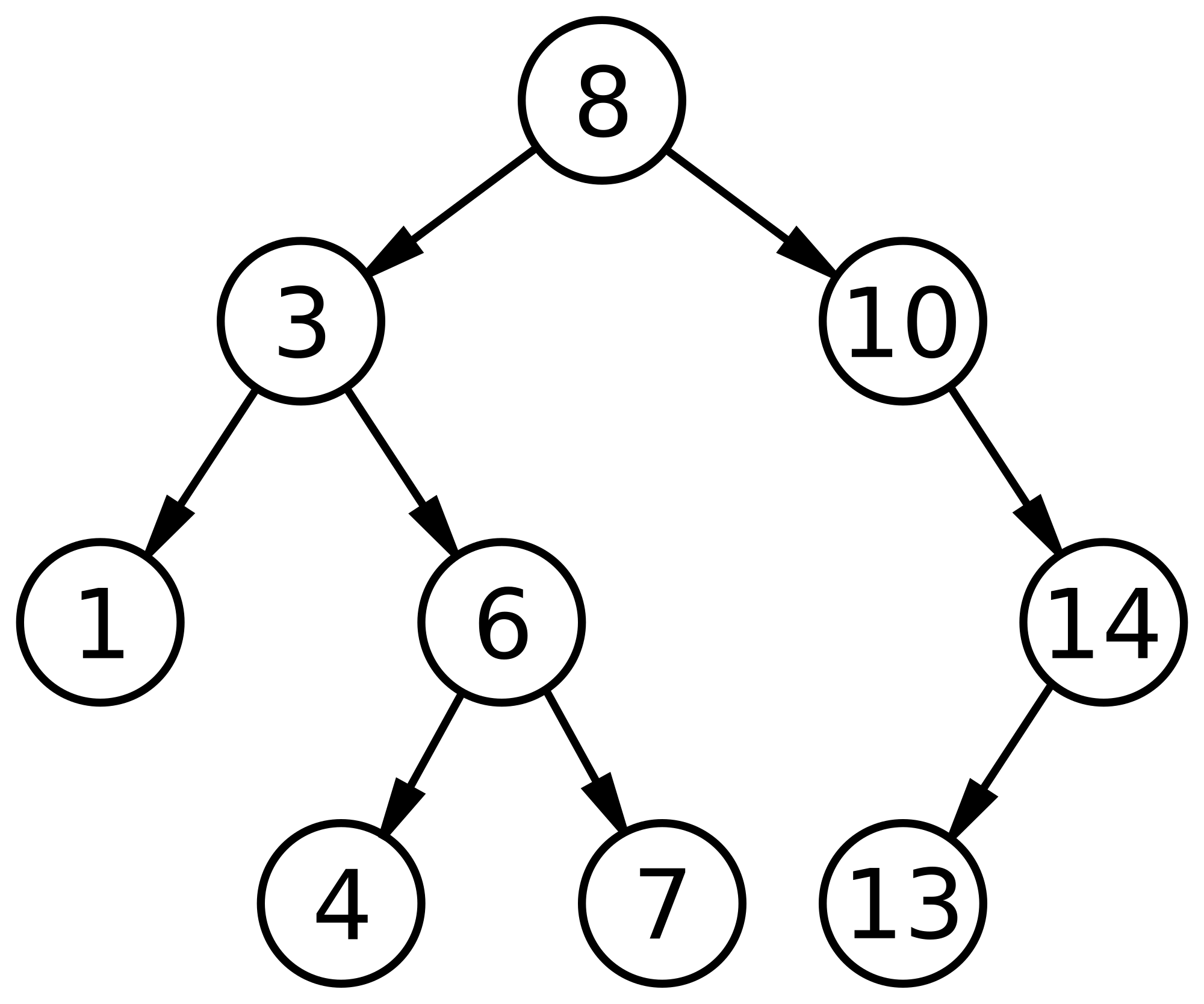
Binary Search Tree adalah tree yang terurut (ordered Binary Tree). Binary Search Tree juga sering disebut dengan Sorted Binary Tree yang berfungsi untuk menyimpan informasi nama atau bilangan yang disimpan di dalam memory. Dengan ini data dibagi menjadi dua dengan mencari titik tengah seagai patokannya. Binary tree terdiri dari simpul utama yang disebut dengan istilah root. Kemudian dari root tersebut terdapat bagian kiri dan bagian kanan. Data disimpan setelah root disimpan berdasarkan nilai perbandingan dengan root tersebut.

Pemakaian tree structure dalam proses pencarian (search)

Binary Search Tree:

Proses pencarian (searching) berbasis binary tree. Tree traversal adalah cara kunjungan node-node pada pohon biner.

Ada tiga cara kunjungan dalam tree:

1. Pre order

a. Cetak data pada root

b. Secara rekursif mencetak seluruh data pada subpohon kiri

c. Secara rekursif mencetak seluruh data pada subpohon kanan