Heaps & Tries
1. Definisi.
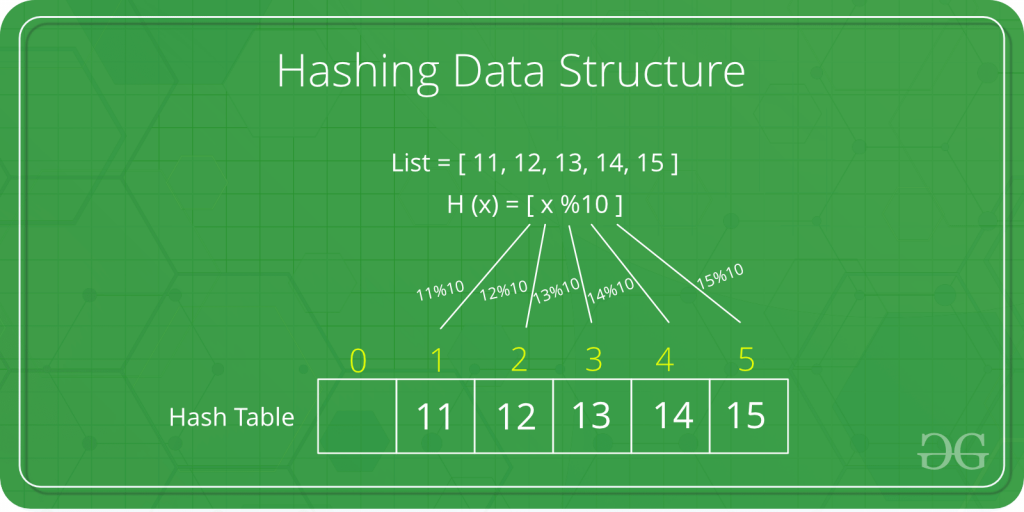
Heap adalah bagian dari memori yang terorganisasi untuk dapat melayani alokasi memori secara dinamis. Heap merupakan struktur data berbasis pohon khusus di mana pohon itu adalah pohon biner yang lengkap.
2. Max Heap
Dalam Max-Heap kunci yang ada di simpul akar harus paling besar di antara kunci yang ada di semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua sub-pohon di Pohon Biner tersebut.
Cara insert:
a. memasukan data dengan konsep array, sehingga kekanan terus lalu kebawah. Elemen terakhir akan masuk ke index terakhir dan menjadi anak paling kanan dan paling bawah.
b. data yang di insert akan dibandingkan dengan parent jika lebih besar maka akan swap. Bandingkan terus sampai data baru lebih kecil dari parent.
Cara delete:
a. jika elemen terkecil terletak di root maka yang akan dihapus adalah element terbesarnya.
b. Root yang dihapus kemudian digantikan oleh data terakhir di nodenya kemudian data tersebut di down heap max sampai node lebih besar dari child node.
3. Min Heap
Dalam Min-Heap kunci yang ada di simpul akar harus minimum di antara kunci yang ada di semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua sub-pohon di Pohon Biner itu.
Cara insert :
a. memasukkan data dengan konsep array, sehingga kekanan terus lalu kebawah. Elemen terakhir akan masuk ke index terakhir dan menjadi anak paling kanan dan paling bawah.
b. data yang sudah dimasukkan lalu dibandingkan dengan parent. Jika data tersebut lebih kecil makan akan di swap. Bandingkan terus sampai data baru lebih besar dari parent.
Cara delete :
a. jika elemen terkecil terletak di root maka yang akan dihapus adalah elemen terkecil.
b. root yang sudah dihapus kemudian digantikan oleh data terakhir pada nodenya.
Lalu data tersebut di down heap min sampai node lebih kecil dari child node.
4. Min-Max Heap
Min-Max Heap adalah heap yang tiap level selalu bergantian Min-Max-Min-Max. dalam Min-Max dan setiap heap selalu di awali dengan min heap. Min- Max Heap berguna untuk langsung menemukan nilai min dan max dalam 1 heap saja. Pada level min semakin kebawah maka nilainya semakin besar. Pada level max semakin kebawah maka nilainya semakin kecil. Kondisi heap selalu bergantian, yaitu level minimal dan maksimal.
-Setiap elemen pada level genap atau ganjil lebih kecil dari semua anak-anaknya (level min).
Cara insert :
a. proses node baru akan dilakukan akan dipengaruhi oleh lokasi node tersebut.
b. jika node baru berada di level min makan akan dibandingkan dengan parentnya. Jika parent lebih kecil dari node baru maka swap dan up heap max dari parent dan akan dibandingkan dengan grandparent dari posisi node baru setelah swap. Jika parent lebih besar dari node baru, up heap min dari posisi node baru akan dibandingkan dengan grandparent dari posisi node baru.
-Setiap elemen pada level ganjil atau genap lebih besar dari semua anak-anaknya (level maks).
Cara insert :
a. proses node baru akan dilakukan dipengaruhi oleh lokasi node baru tersebut.
b. jika node baru berada di level max, maka akan dibandingkan dengan parentnya. Jika parent lebih besar dari node baru maka swap dan up heap min dari parentnya akan dibandingkan dengan grandparentnya dari posisis node baru setelah swap. Jika parent lebih kecil dari node baru up heap max dari posisi node baru akan dibandingkan dengan grandparent dari posos node baru.
5. Implementasi.
Heap tree bermanfaat untuk mengimplementasikan priority queue. Priority queue merupakan struktur data yang sifatnya sangat mirip dengan antrian, yaitu penghapusan/pengurangan anggota selalu dilakukan pada anggota antrian yang terdepan dan penambahan anggota selalu dilakukan dari belakang antrian berdasarkan prioritas anggota tersebut (anggota yang memiliki prioritas lebih besar selalu berada di depan anggota yang memiliki prioritas lebih rendah).
Heap tree memerlukan beberapa metoda sebagai berikut:
a. Metoda untuk menginisialisasi suatu CBT (Complete Binary Tree) A secara umum menjadi heap.
b. Metoda untuk mengambil data paling besar, yaitu root dari heap.
c. Metoda untuk menambahkan satu key baru ke dalam heap tree.
d. Metoda untuk menyusun ulang menjadi heap tree kembali setelah dilakukan metoda B atau C.
Kriteria yang penting untuk dipenuhi adalah bahwa setiap metoda di atas beroperasi pada tree yang selalu berbentuk CBT (Complete Binary Tree) karena struktur level lebih rendahnya tetap merupakan suatu array.
6. Representasi Alokasi Dinamis Algoritma Pengurutan Heap Sort.
Karakteristik dari algoritma pengurutan heap sort adalah bahwa dalam implementasinya heap sort menggunakan heap tree agar dapat diselesaikan secara heapsort. Oleh karena itu, untuk mengimplementasikan algoritma pengurutan heap sort dalam suatu program aplikasi, dibutuhkan adanya alokasi dinamis dengan menggunakan struktur data tree (pohon).
Prinsip-prinsip dasar mengenai struktur data tree yang digunakan untuk merealisasikan heap tree adalah sebagai berikut:
a. Node-node saling berhubungan dengan menggunakan pointer. Pada struktur data tree ini digunakan minimal dua buah pointer pada setiap node, masing-masing untuk menunjuk ke cabang kiri dan cabang kanan dari tree tersebut. Struktur data tree dideklarasikan sebagai berikut:
Class BinaryTreeNode {
KeyType Key;
InfoType Info;
BinaryTreeNode Left, Right;
}
b. Left dan Right berharga NULL apabila tidak ada lagi cabang pada arah yang bersangkutan.
c. Struktur dari binary tree, termasuk hubunganhubungan antar-node, secara eksplisit direpresentasikan oleh Left dan Right. Apabila diperlukan penelusuran naik (backtrack), maka hal tersebut dapat dilakukan dengan penelusuran ulang dari root, penggunaan algoritma-algoritma yang bersifat rekursif, atau penggunaan stack.
d. Alternatif lain adalah dengan menambahkan adanya pointer ke parent. Namun hal ini akan mengakibatkan bertambahnya jumlah tahapan pada proses-proses penambahan/penghapusan node.
Algoritma pengurutan heap sort dapat dikategorikan ke dalam algoritma divide and conquer dengan pendekatan pengurutan sulit membagi, mudah menggabung (hard split/easy join) seperti halnya algoritma pengurutan quick sort dan selection sort. Hal ini disebabkan pembagian dilakukan dengan terlebih dahulu menerapkan algoritma metoda heapify sebagai inisialisasi awal untuk mentransformasi suatu Complete Binary Tree (CBT) menjadi heap tree dan pada setiap tahapan diterapkan algoritma metoda reheapify untuk menyusun ulang heap tree.
7. Tries
Tries adalah tree yang dilakukan untuk menyimpan array asosiatif. Properties yang terdapat di Tries:
-Setiap vertex/node merepresentasikan satu huruf.
-Root merepresentasikan karakter kosong.
-Aplikasi pada trees adalah fitur auto complete yang ada pada web browser.
Struktur data dari tree berututan yang digunakan untuk menyimpan array asosiatif biasanya adalah string. Tries merupakan pohon yang setiap simpulnya mewakili satu kata atau awalan. Root mewakili karakter kosong (‘’). Vertex adalah jarak dari root memiliki awalan yang terkait dengan panjang K. misalkan A dan B adalah dua simpul dari pecobaan. A adalah orangtua dari B, maka B harus memiliki awalan yang terkait dengan A.
AVL TREE
AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dapat dipersingkat dan disederhanakan Walaupun Binary SearchTree sudah dapat mengatasi kelemahan pada Binary Tree dengan cara mengurutkan / sort node yang di-insert, di-update dan di-delete, tetapi masih ada kendala lain yang dihadapai binary search tree , yaitu masih ada kemungkinan terbentuk skewed binary tree (tree miring), yang mempunyai perbedaan height (height-balanced) antara subtree kiri dengan subtree kanan. AVL (Adelson, Velskii dan Landis) Tree mengatasi hal ini dengan cara membatasi height-balanced maksimum 1. AVL Tree dapat didefinisikan sebagai Binary Search Tree yang mempunyai ketentuan bahwa “maksimum perbedaan height antara subtree kiri dan subtree kanan adalah 1”.

Penambahan node di AVL Tree
Untuk menjaga tree tetap imbang, setelah penyisipan sebuah node, dilakukan pemeriksaan dari node baru → root. Node pertama yang memiliki |balance factor| > 1 diseimbangkan. Proses penyeimbangan dilakukan dengan: Single rotation dan Double rotation.
Rotasi AVL Tree
Untuk menyeimbangkan dirinya sendiri, pohon AVL dapat melakukan empat jenis rotasi berikut:
-Rotasi kiri
-Rotasi kanan
-Rotasi Kiri-Kanan
-Rotasi Kanan-Kiri
Dua rotasi pertama adalah rotasi tunggal dan dua rotasi berikutnya adalah rotasi ganda. Untuk memiliki pohon yang tidak seimbang, kita setidaknya membutuhkan pohon dengan ketinggian 2. Dengan pohon sederhana ini, mari kita pahami satu per satu.
Rotasi Kiri:
Jika pohon menjadi tidak seimbang, ketika sebuah simpul dimasukkan ke subtree kanan subtree kanan, maka kita melakukan rotasi kiri tunggal.
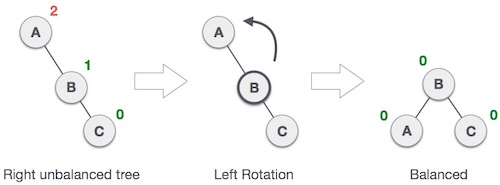
Dalam contoh kami, simpul A menjadi tidak seimbang karena simpul dipasang di subtree kanan subtree kanan A. Kami melakukan rotasi kiri dengan membuat A subtree kiri B.
Rotasi Kanan:
Pohon AVL dapat menjadi tidak seimbang, jika diatur di subtree kiri subtree kiri. Pohon itu kemudian membutuhkan rotasi yang benar.
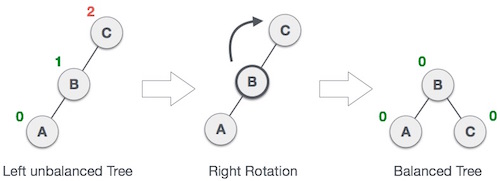
Seperti yang digambarkan, simpul yang tidak seimbang menjadi anak kanan anak kirinya dengan melakukan rotasi kanan.
Insertion node di AVL Tree
Anggap X adalah node yang harus diseimbangkan kembali
– Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri X (left-left)
– Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan X (right-right)
– Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri X (right-left)
– Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan X (left-right)
Untuk memastikan bahwa pohon yang diberikan tetap AVL setelah setiap penyisipan, kita harus menambah operasi penyisipan BST standar untuk melakukan penyeimbangan ulang. Berikut ini adalah dua operasi dasar yang dapat dilakukan untuk menyeimbangkan kembali BST tanpa melanggar properti BST (kunci (kiri) <kunci (root) <kunci (kanan)).
Langkah-langkah yang harus diikuti untuk pemasangan:
Biarkan simpul yang baru dimasukkan menjadi P.
1) Lakukan insert BST standar untuk P
2) Mulai dari P, naik dan temukan simpul tidak seimbang pertama. Biarkan Z menjadi simpul tidak seimbang pertama, Y menjadi anak dari Z yang datang di jalan dari P ke Z dan X menjadi cucu dari Z yang datang di jalur dari P ke Z.
3) Seimbangkan kembali pohon dengan melakukan rotasi yang sesuai pada subtree yang di-root dengan Z. Ada 4 kemungkinan kasus yang perlu ditangani karena X, Y dan Z dapat diatur dalam 4 cara. Berikut ini adalah 4 pengaturan yang mungkin:
a) Y adalah anak kiri dari Z dan X adalah anak kiri dari Y (Left left Case)
b) Y adalah anak kiri Z dan X adalah anak kanan Y (Left Right Case)
c) Y adalah anak kanan Z dan X adalah anak kanan Y (Right Right Case)
d) Y adalah anak kanan Z dan X adalah anak kiri Y (Left right Case)
Anggap T adalah node yang harus diseimbangkan kembali.
– Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
– Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
– Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
– Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)
Deletion node di AVL Tree
Jika node yang akan dihapus berada pada posisi leaf atau node tanpa anak, maka dapat langsung di hapus. Jika node yang akan dihapus memiliki anak, maka proses penghapusannya harus di cek kembali untuk menyeimbangkan Binary Search Tree dengan perbedaan tinggi / level maksimal 1. Proses menghapus sebuah node di AVL tree hampir sama dengan BST. Penghapusan sebuah node dapat menyebabkan tree tidak imbang Setelah menghapus sebuah node, lakukan pengecekan dari node yang dihapus menjadi root. Gunakan single atau double rotation untuk menyeimbangkan node yang tidak imbang. Pencarian node yang imbalance diteruskan sampai root.
Kesimpulan:
Dari rangkuman ini didapatkan kesimpulan bahwa :
1. Dengan menggunakan AVL Tree maka pohon
biner dapat melakukan otomatis penyeimbangan.
2. AVL Tree dapat membuat perbedaan ketinggian
pohon memiliki selisih tinggi maksimal 1.