AVL TREE

AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dapat dipersingkat dan disederhanakan Walaupun  Binary  SearchTree  sudah  dapat mengatasi kelemahan pada Binary Tree dengan cara mengurutkan / sort node yang di-insert, di-update dan di-delete,  tetapi  masih  ada  kendala  lain  yang dihadapai  binary  search  tree ,  yaitu  masih  ada kemungkinan  terbentuk  skewed  binary  tree  (tree miring), yang mempunyai perbedaan height (height-balanced) antara subtree kiri dengan  subtree kanan. AVL  (Adelson,  Velskii  dan  Landis)  Tree mengatasi  hal  ini dengan  cara  membatasi    height-balanced maksimum 1. AVL Tree dapat didefinisikan sebagai  Binary  Search  Tree  yang  mempunyai ketentuan  bahwa  “maksimum perbedaan height antara subtree kiri dan subtree kanan adalah 1”. 

Penambahan node di AVL Tree

        Untuk menjaga tree tetap imbang, setelah penyisipan sebuah node, dilakukan pemeriksaan dari node baru → root. Node pertama yang memiliki |balance factor| > 1 diseimbangkan. Proses penyeimbangan dilakukan dengan: Single rotation dan Double rotation.

              Rotasi AVL Tree

Untuk menyeimbangkan dirinya sendiri, pohon AVL dapat melakukan empat jenis rotasi berikut:

-Rotasi kiri

-Rotasi kanan

-Rotasi Kiri-Kanan

-Rotasi Kanan-Kiri

Dua rotasi pertama adalah rotasi tunggal dan dua rotasi berikutnya adalah rotasi ganda. Untuk memiliki pohon yang tidak seimbang, kita setidaknya membutuhkan pohon dengan ketinggian 2. Dengan pohon sederhana ini, mari kita pahami satu per satu.

Rotasi Kiri

Jika pohon menjadi tidak seimbang, ketika sebuah simpul dimasukkan ke subtree kanan subtree kanan, maka kita melakukan rotasi kiri tunggal.

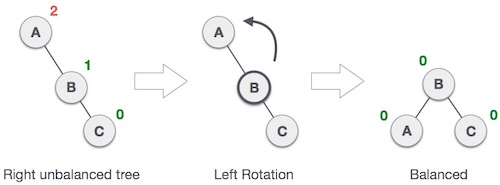
Dalam contoh kami, simpul A menjadi tidak seimbang karena simpul dipasang di subtree kanan subtree kanan A. Kami melakukan rotasi kiri dengan membuat A subtree kiri B.

Rotasi Kanan

Pohon AVL dapat menjadi tidak seimbang, jika diatur di subtree kiri subtree kiri. Pohon itu kemudian membutuhkan rotasi yang benar. 

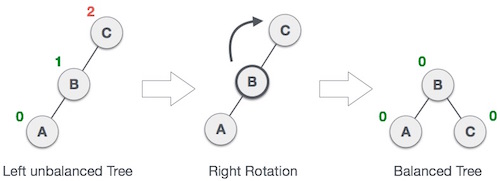
Seperti yang digambarkan, simpul yang tidak seimbang menjadi anak kanan anak kirinya dengan melakukan rotasi kanan.  

Insertion node di AVL Tree

Anggap X adalah node yang harus diseimbangkan kembali

– Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri X (left-left)

– Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan X (right-right)

– Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri X (right-left)

– Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan X (left-right)

Untuk memastikan bahwa pohon yang diberikan tetap AVL setelah setiap penyisipan, kita harus menambah operasi penyisipan BST standar untuk melakukan penyeimbangan ulang. Berikut ini adalah dua operasi dasar yang dapat dilakukan untuk menyeimbangkan kembali BST tanpa melanggar properti BST (kunci (kiri) <kunci (root) <kunci (kanan)).

1) Rotasi Kiri

2) Rotasi Kanan 

Langkah-langkah yang harus diikuti untuk pemasangan

Biarkan simpul yang baru dimasukkan menjadi P

1) Lakukan insert BST standar untuk P

2) Mulai dari P, naik dan temukan simpul tidak seimbang pertama. Biarkan Z menjadi simpul tidak seimbang pertama, Y ​​menjadi anak dari Z yang datang di jalan dari P ke Z dan X menjadi cucu dari Z yang datang di jalur dari P ke Z.

3) Seimbangkan kembali pohon dengan melakukan rotasi yang sesuai pada subtree yang di-root dengan Z. Ada 4 kemungkinan kasus yang perlu ditangani karena X, Y dan Z dapat diatur dalam 4 cara. Berikut ini adalah 4 pengaturan yang mungkin:

a) Y adalah anak kiri dari Z dan X adalah anak kiri dari Y (Left left Case)

b) Y adalah anak kiri Z dan X adalah anak kanan Y (Left Right Case)

c) Y adalah anak kanan Z dan X adalah anak kanan Y (Right Right Case)

d) Y adalah anak kanan Z dan X adalah anak kiri Y (Left right Case)

Anggap T adalah node yang harus diseimbangkan kembali.

– Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)

– Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)

– Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)

– Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)

Deletion node di AVL Tree
Jika node yang akan dihapus berada pada posisi leaf atau node tanpa anak, maka dapat langsung di hapus. Jika node yang akan dihapus memiliki anak, maka proses penghapusannya harus di cek kembali untuk menyeimbangkan Binary Search Tree dengan perbedaan tinggi / level maksimal 1. Proses menghapus sebuah node di AVL tree hampir sama dengan BST. Penghapusan sebuah node dapat menyebabkan tree tidak imbang Setelah menghapus sebuah node, lakukan pengecekan dari node yang dihapus  menjadi root. Gunakan single atau double rotation untuk menyeimbangkan node yang tidak imbang. Pencarian node yang imbalance diteruskan sampai root.

Kesimpulan 
Dari  rangkuman  ini  didapatkan  kesimpulan bahwa :
1. Dengan  menggunakan  AVL  Tree  maka  pohon
biner dapat melakukan otomatis penyeimbangan.
2. AVL Tree dapat membuat perbedaan ketinggian
pohon memiliki selisih tinggi maksimal 1.

Kesimpulan

Dari penelitian ini didapatkan kesimpulan

bahwa :

1. Dengan menggunakan AVL Tree maka pohon

biner dapat melakukan otomatis penyeimbangan.

2. AVL Tree dapat membuat perbedaan ketinggian

pohon memiliki selisih tinggi maksimal 1.